| Lazy Propagation 이란? |
기존 세그먼트 트리에서 i 에서 j 까지의 구간을 업데이트 하기 위해서는 수행시간은 O(NlogN)의 시간이 걸리게 된다.
이 구간 없데이트 시간을 단축 시키기 위한 알고리즘이 필요한데 이때 사용하는 알고리즘이 Lazy Propagation(게으르게 전파) 알고리즘이다. 이 알고리즘의 수행 속도는 O(logN) 이다.
| Lazy Propagation 동작 방법 |
배열 {1,2,3,4,5} 가 있는 구간합의 예를 살펴 봅니다.
세그먼트 트리 구현시 다음과 같은 트리가 생성 됩니다.

이때 0번지 부터 2번지까지에 3을 더해 준다고 하면 다음과 같이 계산이 됩니다.
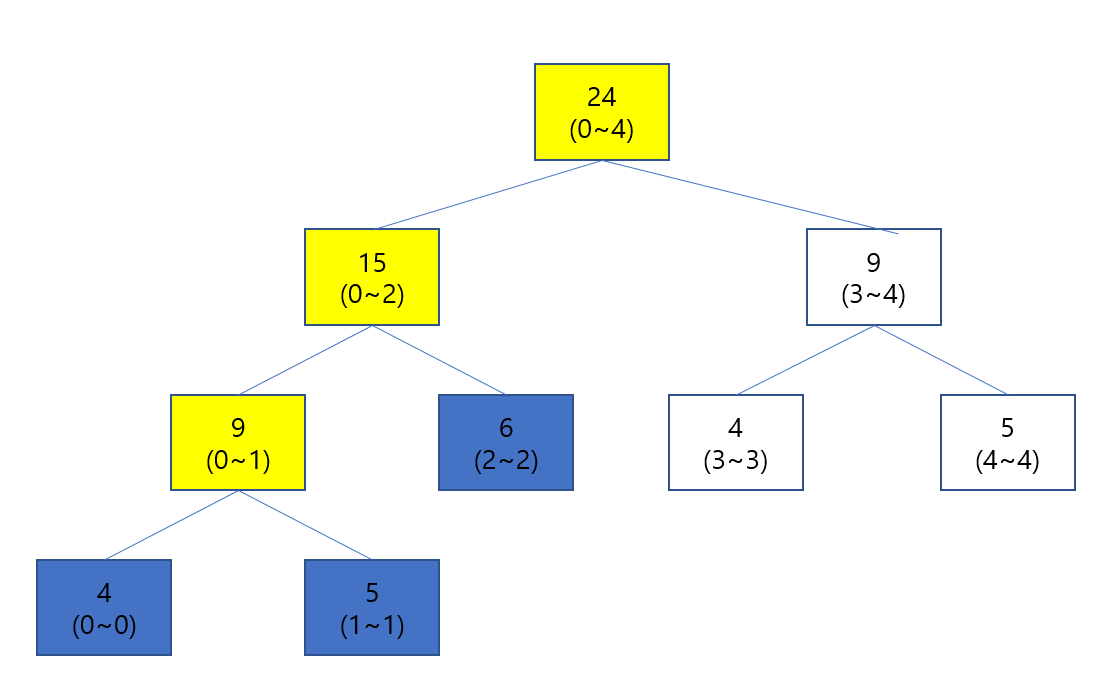
파랑색 부분을 계산하면서 노랑색 부분은 (0~1) 위치는 2번, (0~2) 위치는 3번, (0~4) 위치는 3번 이 계산 됩니다.
따라서 업데이트 소요 시간은 NlogN 의 시간의 소요가 발생합니다.
여기서 Lazy Propagation 의 동작은 다음과 같습니다.
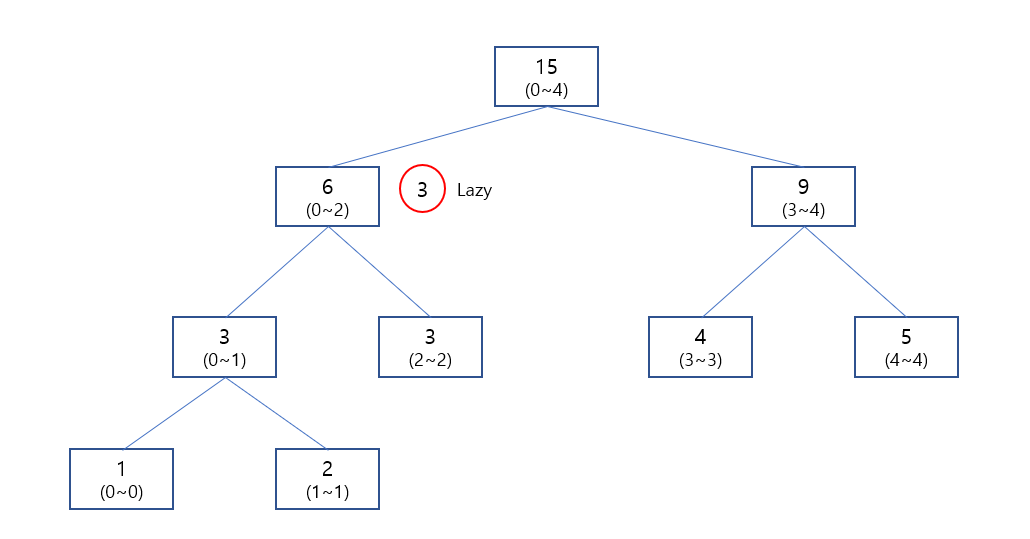
먼저 구간합이 일어나는 0~2 까지의 구간위치에 Lazy 값 3을 입력 합니다.
이렇게 Lazy 값을 셋팅 해주고 2번지 부터 4번지까지의 쿼리를 해 보도록 하겠습니다.

이 구간의 구간합은 6 + 4 + 5 = 15의 값이 나와야 합니다.
이때 방문하는 위치를 보면 다음과 같이 노란색 위치가 됩니다.

여기서 쿼리를 위해 자신을 방문할때 하위노드에 Lazy 값을 반영 후에 자신의 Lazy 값을 삭제 합니다.

이렇게 계산을 한 후에 6 + 9 의 15 값을 가져 올 수 있습니다.
하지만 문제는 상위에 적용이 안되는 부분이 있는데 이 부분은 업데이트 과정에서 빠져 나오면서 적용을 할 수가 있습니다.
그러면 업데이트 과정을 다시 한번 살펴 보겠습니다.
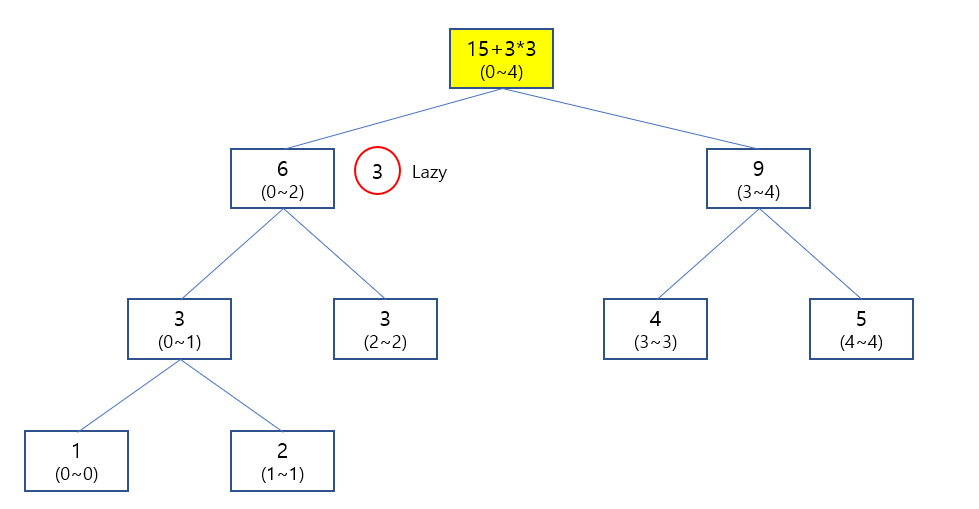
0~2번지에 3의 값을 누적하는 상황이 된다면

위와 같이 3의 Lazy 값을 셋팅 후에 나오면서 0~4 구간에 3 * 3 의 값을 셋팅 해 줄수가 있습니다.
| 문제풀이 |
10999번: 구간 합 구하기 2
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
|
#include <iostream>
#include <stdio.h>
#define MAXN 1000010
using namespace std;
struct Data{
long long sum;
long long Lazy;
};
int N,M,K;
Data SegTree[1<<21]; //세그먼트 트리 갯수는 2,097,152 개 이상이어야 한다.
void updataSegTree(int cur,int s,int e,int pos,int val)
{
if(s==e){
SegTree[cur] = {val,0}; ///내 위치를 찾아 왔으면 업데이트 하자.
return;
}
int mid = (s+e)/2;
if(mid<pos) updataSegTree(cur*2 + 1,mid+1,e,pos,val); ///오른쪽 자식위치로 이동
else updataSegTree(cur*2,s,mid,pos,val); ///왼쪽 자식 위치로 이동
SegTree[cur].sum = SegTree[cur*2].sum + SegTree[cur*2 + 1].sum; ///자식의 합을 누적
}
void updataLazeTree(int cur,int rangestart,int rangeend,int s,int e,long long val)
{
//lazy가 남아있을 때
if(SegTree[cur].Lazy != 0){
SegTree[cur].sum += (rangeend-rangestart+1)*SegTree[cur].Lazy;
if(rangestart != rangeend){
SegTree[cur*2].Lazy += SegTree[cur].Lazy;
SegTree[cur*2+1].Lazy += SegTree[cur].Lazy;
}
SegTree[cur].Lazy =0;
}
if(e < rangestart || s > rangeend) return; //범위를 벗어날때
if(s <= rangestart && rangeend <= e){ //현재 범위가 구간의 포함되는 경우
SegTree[cur].sum += (rangeend-rangestart+1)*val;
if(rangestart != rangeend){
SegTree[cur*2].Lazy += val;
SegTree[cur*2+1].Lazy += val;
}
return;
}
updataLazeTree(cur*2, rangestart, (rangestart+rangeend)/2, s, e, val);
updataLazeTree(cur*2+1, (rangestart+rangeend)/2+1, rangeend, s, e, val);
SegTree[cur].sum = SegTree[cur*2].sum+SegTree[cur*2+1].sum;
}
long long queryLazeTree(int cur,int rangestart,int rangeend,int s,int e)
{
if(SegTree[cur].Lazy != 0){
SegTree[cur].sum += (rangeend-rangestart+1)*SegTree[cur].Lazy;
if(rangestart != rangeend){
SegTree[cur*2].Lazy += SegTree[cur].Lazy;
SegTree[cur*2+1].Lazy += SegTree[cur].Lazy;
}
SegTree[cur].Lazy =0;
}
if(s> rangeend || e < rangestart) return 0;
if(s <= rangestart && rangeend <= e)
return SegTree[cur].sum;
return queryLazeTree(cur*2, rangestart, (rangestart+rangeend)/2, s, e)+queryLazeTree(cur*2+1, (rangestart+rangeend)/2+1, rangeend, s, e);
}
int main()
{
//freopen("input.txt","r",stdin);
cin.tie(NULL);
cout.tie(NULL);
ios::sync_with_stdio(NULL);
int num;
cin >> N >> M >> K;
for(int i=1;i<=N;i++)
{
cin >> num;
updataSegTree(1,1,N,i,num);
}
int cmd;
int a,b,c;
for(int i=0;i<M+K;i++)
{
cin >> cmd;
if(cmd==1)
{
cin >> a >> b >> c;
updataLazeTree(1,1,N,a,b,c);
}
else{
cin >> a >> b;
cout << queryLazeTree(1,1,N,a,b) << "\n";
}
}
return 0;
}
|
cs |
오늘도 최선을 다하는 우리 학생들을 응원합니다.
인천 서구 검단신도시 원당컴퓨터학원
'강의자료 > 알고리즘' 카테고리의 다른 글
| [자료구조]세그먼트트리(Segment Tree) (15) | 2021.11.26 |
|---|---|
| 기하 알고리즘] 두 원의 겹치는 영역의 넓이 구하기 (8) | 2021.09.03 |
| [알고리즘] convex hull trick (0) | 2020.12.25 |
| [자료구조] 우선순위큐(Priority Queue) (0) | 2020.11.17 |
| [자료구조]링크드 리스트(Linked List) (0) | 2020.11.17 |