| Convex Hull trick 란 |
Convex Hull trick 란 Convex Hull(블록껍질) 알고리즘과는 다른 알고리즘이다.
최적의 값을 찾아가는 형태가 Convex Hull 을 닮아서 Convex Hull trick 라고 알려져 있는데~
Convex Hull Optimization 이라고도 한다.
이 알고리즘은 특정 점화식 꼴을 가지는 동적계획법에서 시간을 줄이는 방법이다.
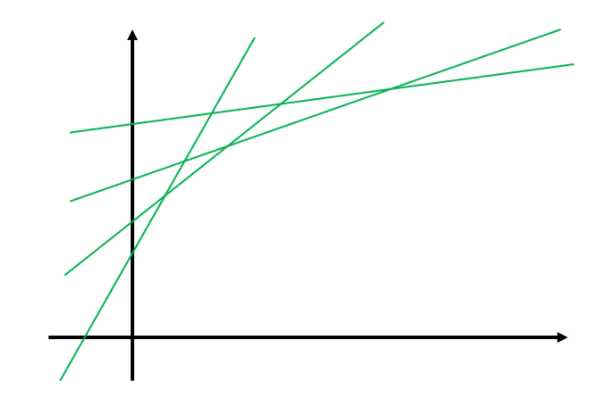
일차 함수식이 위와 같이 여러개가 들어 오는 경우
각 x의 입장에서 최솟값을 찾는 알고리즘
동적알고리즘에서 다음과 같은 형태의 점화식 작성시 사용됨
dp[i] = min(dp[j] + a[i]b[j])( 0<=j < i)
여기서 y = ax + b 와 같은 형태를 띄게 되는데
a[i] 는 x 에 해당하는 상수값을 의미
b[j] 는 a에 해당하는 j값에 의해 변하는 값을 의미
dp[j] 는 각 직선에서 b 에 해당하는 변하는 값을 의미
여기서 x는 고정값이고 a와 b 의 값이 변하는 값인데 해당하는 x 값 위치에서 가장 최선의 a와 b를 찾는 것이 Convex Hull Trick 알고리즘이다.
구현 방법은 아래 문제를 해결하면서 확인을 하자.
| 문제풀이 |
백준- www.acmicpc.net/problem/13263
13263번: 나무 자르기
첫째 줄에 n(1 ≤ n ≤ 100,000)이 주어진다. 둘째 줄에는 a1, a2, ..., an이, 셋째 줄에는 b1, b2, ..., bn이 주어진다. (1 ≤ ai ≤ 109, 0 ≤ bi ≤ 109) a1 = 1이고, bn = 0이며, a1 < a2 < ... < an, b1 > b2 > ... > bn을 만족
www.acmicpc.net
나무자르기 문제가 대표적인 Convex Hull Trick 을 사용하는 문제이다.
이 문제를 처음 접할때 이게 왜 직선의 방정식인지 이해가 안 가는 경우가 발생을 하는데~
이 문제의 두번째 예를 살펴 보자
5
1 2 3 10 20 30
6 5 4 3 2 0
이 문제를 풀기 위해서 접근을 해 보면
1의 나무를 자르는데는 비용이 발생하지 않지만 1의 나무를 잘라야만 충전을 할 수가 있기 때문에 1을 먼저 잘라야 한다.
30의 나무를 자르고 나면 그 다음 부터는 0의 비용으로 나무를 자를 수 있다.
따라서 1의 나무를 먼저 자른후에 30을 자른다고 하면 30을 자르는 비용은 6 * 30 = 180 의 비용이 된다.
그 다음 부터는 0의 비용으로 충전을 할 수 있으므로 180의 충전 비용으로 나무를 모두 자를수 있다.
그런데 그것이 가장 좋은 방법일까?
1을 먼저 자른후
2를 자르는 비용을 생각하자 => 2 * 6= 12
3을 자르는 비용을 생각하자 => 12 + (3*5) = 27 또는 3 * 6 = 18 중 작은 값 18을 선택 할 수 있다.
10을 자르는 비용을 생각하자 => 18 + (10*4) = 58 또는 12 + (10*5) = 62 또는 10 * 6 = 60 중에서 58을 선택 할 수 있다.
20을 자르는 비용을 생각하자 => 58 + (20*3) = 118 또는 18 + (20*4) = 98 또는 12 + (20*5) = 112 또는 (20*6) = 120 중에서 98 을 선택 할 수 있다.
30을 자르는 비용을 생각하자 => 98 + (30*2) = 158 또는 58 + (30*3) = 148 또는 18 + (30*4) = 138 또는 12 + (30*5) = 162 또는 30* 6= 180 중에서 가장작은 138을 선택 할 수 있다.
이렇게 생각해 보면 다이나믹인것을 확인 할수 있다.
dp[i] = min(dp[j] + a[i]b[j]) 와 같은 형식이 되는 것을 확인 할 수 있다.
하지만 i의 크기가 100000 이라서 이렇게 다이나믹으로 해결 할때 시간초과가 발생하는 것을 알 수 있다.
하지만 점화식이 좀전에 설명한 Convex Hull Trick 에 해당하는 직선의 방정식으로 표현 되는 것을 확인 할 수 있다.
y=ax + b 와 같은 직선의 방정식에서 해당 x의 위치에서 a와 b의 최적값을 찾는 데 이때는 이진탐색을 사용해서 해결할 수가 있다.
소스코드를 살펴 보면 다음과 같이 해결이 가능하다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
|
#include <iostream>
#include <vector>
#include <algorithm>
#define MAX 100010
using namespace std;
struct Line{
long long a,b; // y=ax+b 형태의 a,b 값
double crossPos; // 앞에 나오는 라인과 만나는 x 위치중에서 가장 작은 x 값을 저장하자.
};
vector <Line> S;
int a[MAX],b[MAX],n;
long long dp[MAX];
double cross(const Line &l,const Line &r)
{
/// left 와 right 가 서로 만나는 지점을 찾는 것이므로
/// l.a * x +l.b = r.a * x + r.b 이다
/// x = (r.b - l.b)/(l.a-r.a) 이다.
return (r.b - l.b)/(l.a - r.a);
}
int main()
{
cin.tie(NULL);
cout.tie(NULL);
ios::sync_with_stdio(NULL);
freopen("input.txt","r",stdin);
cin >> n;
for(int i=0;i<n;i++) cin >> a[i];
for(int i=0;i<n;i++) cin >> b[i];
/// 0번 위치의 값은 비용이 들지 않으므로 1번 부터 계산해 주면 된다.
Line imsi;
for(int i=1;i<n;i++){
imsi.a = b[i-1]; /// min(dp[j] + a[i]b[j] 에서 y = ax + b 형태에서 a에 해당하는 값은 b[j] 에 해당한다.
imsi.b = dp[i-1]; /// b에 해당하는 값은 dp[j] 에 해당한다.
imsi.crossPos = 0;
while(S.size()>0)
{
///기존에 들어온 라인이 있다면 가장 마지막에 입력된 라인과의 교점을 구해 보자.
imsi.crossPos=cross(imsi,S.back());
if(imsi.crossPos<S.back().crossPos)
{
S.pop_back(); /// 자신과 만나는 위치가 그 이전에 만나는 값보다 더 작다고 하면 굳이 있을 필요가 없다.
}
else break;
}
S.push_back(imsi);
long long x= a[i];
int pos =0;
int left=0;
int right=S.size() -1;
int mid;
/// 현재 버퍼에서 가장 가까운 값을 찾아서 dp 테이블에 넣어 주자.
while(left<=right)
{
mid = (left+right)/2;
if(S[mid].crossPos < x)
{
pos = mid; /// 만나는 점이 내 위치보다 작다면 일단 선택해 주자.
left = mid+1;
}
else
{
right = mid - 1;
}
}
dp[i]=S[pos].a * x + S[pos].b;
}
cout << dp[n-1];
return 0;
}
|
cs |
if(imsi.crossPos<S.back().crossPos)
{
S.pop_back(); /// 자신과 만나는 위치가 그 이전에 만나는 값보다 더 작다고 하면 굳이 있을 필요가 없다.
}
부분의 의미는
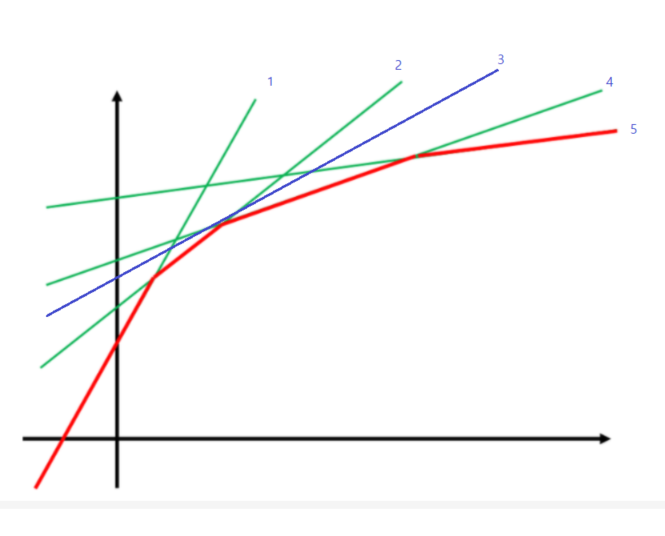
위의 그림에서 3번과 4번을 살펴 보면 3번이 그 이전에 2번을 만나는 위치가 4번이 3번을 만나는 위치보다 더 크기 때문에 굳이 3번 라인을 살펴볼 필요는 없다.
이렇게 하면 x값으로 정렬되어 있는 데이터가 들어갈 수 밖에 없으므로 가장 적합한 위치의 값을 이진탐색으로 탐색이 가능하다.
인천 서구 검단신도시 원당컴퓨터학원
'강의자료 > 알고리즘' 카테고리의 다른 글
| 기하 알고리즘] 두 원의 겹치는 영역의 넓이 구하기 (8) | 2021.09.03 |
|---|---|
| [알고리즘] Lazy Propagation 알고리즘 (6) | 2021.02.22 |
| [자료구조] 우선순위큐(Priority Queue) (0) | 2020.11.17 |
| [자료구조]링크드 리스트(Linked List) (0) | 2020.11.17 |
| [알고리즘]알고리즘 수행시간을 비교해 볼까? (0) | 2020.11.17 |