
조합은 Combination 이라고 하며 순서를 생각하지 않고 나열하는 경우를 말한다.
즉 123 과 321 은 같은 경우로 생각하는 경우이다.
이러한 문제는 중고등부 유형이나 혹은 알고리즘 유형에서 나오는 문제이다.
다음의 문제를 풀어 보자.

문제풀이)
1) 남자 13명 중에서 3명을 뽑는 경우의 수는
첫번째 13명중에서 1명을 뽑는 13가지
두번째 첫번째 뽑힌 사람을 제외하고 12명 중에서 1명을 뽑는 12가지
세번째 는 남은 11명 중에서 1명을 뽑는 11가지
즉 13P3 = 1716 이다.
여기서 남자에게 번호를 1~13까지 번호를 붙여 본다면 1번,2번,3번을 선택한 경우는
123,132,213,231,312,321 과 같이 6가지이다. 하지만 이렇게 6가지의 경우는 동일하게 하나로 선택한 경우이므로 이렇게 순서를 나열 할 수 있는 3! 로 나누는 경우가 조합이다.
따라서 13C3 = 13P3 / 3! = 1716 / 6 = 286
여성 10명 중에서 3명을 뽑는 경우는 위와 같은 경우를 생각하면 10C3 = 10P3/3! = 720/6 = 120
따라서 남자 13명 중에 3명을 뽑는 경우와 여자 10명중 3명을 뽑는 경우는 곱의 법칙이므로 286 * 120 = 34320
2) 전체 23명 중에서 5명을 선택하는 경우 23C5 = 23P5/5! = 106264037880/120 = 33649
여기서 남자만 5명이 선택되는 경우 13C5=1287 와
여자만 5명이 선택되는 경우 10C5=252 인 경우를 빼 주면 된다.
33649 - 1287 - 252 = 32110
3) A남성회원과 B여성회원을 먼저 선택 한 후 나머지 사람 21명 중에서 4명을 선택하는 경우의 수이다.
따라서 21C4 = 5985
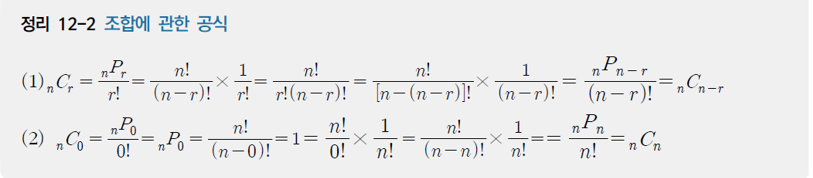


문제풀이)
1) 15명중에서 5명을 선택하는 경우의 수 15C5
남은 10명 중에서 4명을 선택하는 경우의 수 10C4
남은 6명 중에서 3명을 선택하는 경우의 수 6C3
남은 3명 중에서 2명을 선택하는 경우의 수 3C2
남은 1명 중에서 1명을 선택하는 경우의 수 1C1
각각의 그룹은 구성원수가 다르므로 곱의 법칙에 의해서 15C5 * 10C4 * 6C3 * 3C2 * 1C1 = 37837800
2) 15명중에서 4명을 선택하는 경우의 수 15C4
11명 중에서 4명을 선택하는 경우의 수 11C4
7명 중에서 2명을 선택하는 경우의 수 7C2
5명 중에서 2명을 선택하는 경우의 수 5C2
3명 중에서 2명을 선택하는 경우의 수 3C2
1명 중에서 1명을 선택하는 경우의 수 1C1
여기서 4명 그룹이 2개인데 4명 그룹의 순서가 바뀌어도 상관이 없기 때문에 2! 로 나누어 주어야 한다.
또한 2명 그룹이 3개인데 2명 그룹의 순서가 바뀌는 3! 의 경우도 순서에 무관하므로 3!로 나누어 주어야 한다.
따라서 15C4 * 11C4 * 7C2 * 5C2 * 3C2 * 1C1/(3!*2!)=23648625
3) 15C5 * 10C5 * 5C5 / 3! = 126126

중복조합은 중국집에 손님이 오는 경우를 많이 생각하게 되는데~
중국집에 메뉴가 짜장면,짬뽕,탕수육,팔보채,양장피 가 있는데 손님이 3명이 들어 왔습니다.
이때 손님이 주문 할 수 있는 경우는 모두 몇가지인지 구분할때 많이 사용하는데요.
123 번 손님이 모두 짜짜짜, 혹은 짜짜짬, 짜짬탕 등과 같은 형식으로 분리를 하다 보면 정신이 아득해 질 수 있겠는데요.
그렇다면 어떤 식으로 정리를 해 볼까요?
손님이 3명이므로 손님을 ⓐⓑⓒ 라고 하면
ⓐⓑⓒ 를 각 메뉴에 배치 시키는 경우를 생각해 봅니다. 짜짬탕팔양을 그냥 숫자로 생각하면 1,2,3,4,5 로 생각하면
세명을 모두 1에 배치하는 경우가 있을 수 있고 2명을 1에 배치하고 1명을 2에 배치하는 경우가 있을 수 있습니다.
따라서 1,2,3,4,5 사이에 칸막이를 막아 둔다고 하면 1|2|3|4|5 이렇게 칸막이가 4개가 생길것입니다.
이 칸막이 사이에 3명을 배치하는 경우를 그림을 그려보면 짜짜짜를 시키는 경우
ⓐⓑⓒ|||| 과 같이 돠고 짜짜짬을 시키는 경우 ⓐⓑ|ⓒ||| 과 같은 형태가 됩니다.
이렇게 확인을 해 보면 7개 중에서 3개를 선택하는 경우와 동일하게 됩니다.
(ⓐⓑⓒ를 123 으로 생각하고 칸막이를 4567 으로 생각해서 7 중에서 3개를 선택해서 가령 124 를 선택했다고 가정하면 ⓐⓑ|ⓒ||| 와 같은 형태이며 127을 선택했다고 하면 ⓐⓑ||||ⓒ과 같은 형태가 되는것입니다.-해당 번호 위치에 손님이 들어가는 형태)
즉 5-1개(칸막이 갯수) + 3(선택갯수) 중에서 3개를 선택하는 경우의 수 (5-1)+3 C 3 의 경우이며 이것을 5H3 으로 선택을 합니다.
조합에서는 3C5 와 같은 경우가 없지만 중복조합에서는 3H5 가 가능하다는 점도 알아 두면 좋을것 같네요.

문제풀이)
4H3 = (4-1)+3 C 3 = 6C3 = 6*5*4/3*2*1 = 20가지

문제풀이)
기명투표인 경우에는 사람의 이름이 들어 가기 때문에 어떤 회원이 어떤 사람을 선택했는지를 알수 있다.
따라서 이 경우는 1번 투표하는 사람이 3명중에 한명을 선택하는 경우, 2번 투표하는 사람이 3명중에 한명을 선택하는 경우.... 와 같이 되기 때문에 중복 순열에 해당한다.
따라서 3Π15 = 3^15 = 14348907
무기명투표인 경우에는 사람의 이름이 무의미하기 때문에 이 경우는 중복조합에 해당한다.
후보 3명에 칸막이를 만들고 15명을 그 칸막이에 넣을 수 있는 경우이므로
3H15 = (3-1)+15 C 15 = 17C15 = 17C2 = 136
[역대 기출문제]
https://docs.google.com/forms/d/e/1FAIpQLSc6Tvpjb_3JRxK26nzuu1PFXu-_MUiaGKWrCXYNsUWPfoLvwg/viewform
9-1. 조합에 관한 문제
docs.google.com
'강의자료 > 이산수학문제풀이' 카테고리의 다른 글
| [정보올림피아드대비]10. 약수,배수,최대공약수,최소공배수를 이용한 문제 (8) | 2022.06.28 |
|---|---|
| [정보올림피아드대비]9. 나누어 떨어짐을 이용하는 문제(배수판정법) (13) | 2022.05.13 |
| [정보올림피아드대비]7. 순열에 관한 문제(곱의법칙,합의법칙) (9) | 2022.04.26 |
| [정보올림피아드대비]6.숫자로 진 만들기(복면산연산) (10) | 2022.04.14 |
| [정보올림피아드대비]5. 기하문제-평면 (11) | 2022.04.07 |