오늘은 우리 원의 학생이 다음의 문제를 가져 왔네요.^^
(문제는 올림피아드 초등수학 바이블에 나온 문제입니다.)


이 두개의 식을 만족하는 A와 B를 찾는 문제였는데 모든 수를 다 알수가 없다 보니 막막할 수밖에 없네요.
일단 이 식에서 먼저 찾은 수는 다음의 수 입니다.

여기서 10xx 와 아래 9 가 될 수 밖에 없는 이유는 (1) 위치가 1x 인경우만 바로 아래 한자리 숫자를 뺄때 한자리가 되는 경우이기 때문입니다.
따라서 1이 되는 수는 맨 위에 10 에서 9를 빼는 것 외에는 방법이 없습니다.
그러면 A * x 가 9 가 되는 경우는 다음과 같은 경우가 있을 수 있습니다.
(A,x) = (1,9),(3,3)(9,1) 이 3가지 경우를 제외하고는 없는데요 여기서 A는 1일수가 없습니다.
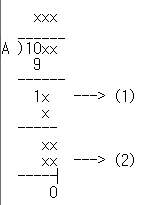
(2)의 위치에서 2자리 숫자가 나와 줘야 하기 때문입니다.
따라서 A=3,9 이 되는 경우 밖에는 없게 됩니다.
여기서 A=3 이 있는 경우 한번 찾아 보겠습니다.

이렇게 A를 구했는데요
그렇다면 B의 위치를 보면 다음과 같겠네요.

여기서 B * x = 10 이 되어야 하는데 이렇게 되는 경우의 쌍은 다음과 같습니다.
(B,x) = (2,5),(5,2) 이 두가지 외에는 없게 됩니다.
따라서 B에 2를 넣어 보면 위의 몫은 20x 가 되며
x의 자리에는 5,6,7,8,9 까지 들어 올수 있으며
x가 5일때 1010
x가 6일때 1012
x가 7일때 1014
x가 8일때 1016
x가 9일때 1018
이렇게 되는 것을 확인 할수가 있어서
이 값을 A쪽에 넣어 보면

1010 인 경우는 (2)의 위치에서 3의 배수가 0으로 끝나는 경우는 없습니다.
1012 인 경우는 (2)의 위치에서 3의 배수가 2로 끝나는 경우 12가 있는데 이때는 (1) 위치에서 10 - 9 인 경우밖에 없기 때문에 1002 이어야 하는데 그렇게 될수가 없습니다.
1014인 경우는 (2)의 위치에서 3의 배수가 4로 끝나는 경우 24 가 있을 수 있습니다.
따라서 (1)의 위치에서 11 - 9 가 되어 24가 될 수 있으므로

위와 같이 두 공식을 채울 수 있습니다.
나머지 1016 역시 3의 배수가 두자리 숫자중 6으로 끝나는 경우가 없고
1018 인 경우 3의 배수가 두자리 숫자중 8로 끝나는 경우가 18 밖에 없기 때문에 불가능합니다.
다시 (B,x) = (5,2) 인 경우를 살펴 보겠습니다.

이때 20X에서 X는 2부터 9까지 가능합니다.
이때 마지막 자리는 0 또는 5로 끝나게 되는데 이때 A가 3인 경우 3의 배수가 0 으로 끝나는 두자리수는 없고 5로 끝나는 두자리수는 15밖에 없기 때문에 A의 두자리가 앞에 1이 나올 수 없으므로 불가능하다.
다음으로 A = 9 인 경우 를 생각해 보면 다음과 같습니다.

이때 B는 동일하게 2 또는 5인 값이 나오며 2일때 마지막 두자리가 동일하게 10,12,14,16,18 이 되는데 이때 A에서 9의 배수가 되는 경우는 18 밖에 없는데 A에서 앞자리가 1이 될수는 없습니다.
따라서 B는 2일 수는 없습니다.
B가 5인경우 10,15,20,25,30,35,40,45 가 있는데 이때 9의 배수가 되는 경우는 45 값이 있을 수 있습니다.
이때 A의 위치의 값은 다음과 같을수 있습니다.

따라서 B의 값은

이렇게 두가지 경우가 나올 수 있습니다.
A=3,B=2 1014
A=9,B=5 1045
복면산 연산은 예전 정보올림피아드 기출문제 유형에서 종종 나왔던 유형인데 이 경우 해법은 딱히 없고~
모든 경우를 하나씩 대입해 보면서 불가능한 경우를 제거해 나가는 방법 밖에는 없습니다.
이런 유형의 문제도 여러번 풀어 보다 보면 실마리를 잡는 연습이 되기 때문에 다양한 문제를 접해 보는 것도 좋은것 같네요.
오늘도 최선을 다하는 우리 학생들을 응원합니다.
인천 서구 원당컴퓨터학원
'강의자료 > 알고리즘 수학' 카테고리의 다른 글
| [컴퓨팅 사고력]해시(Hash)테이블 이해하기 (6) | 2021.02.15 |
|---|---|
| [컴퓨팅 사고력] 피보나치 수열 (5) | 2021.02.01 |
| [초등 사고력 풀이비법] 합과 차의 관계를 이용해 해결하기 (5) | 2021.01.28 |
| [컴퓨팅 사고력]블록쌓기 게임으로 스택 구조 이해하기 (9) | 2021.01.11 |
| [컴퓨팅 사고력]카드 마술에서 배우는 이진법 (4) | 2020.08.17 |